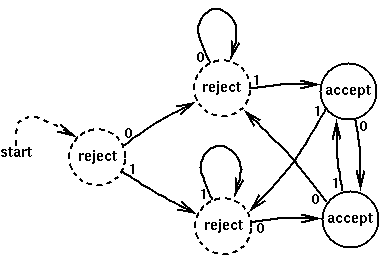This DFA accepts
strings of 0's and 1's which end with either "01" or
"10". For instance, the strings
"10",
"001",
"101",
"110",
"01010",
"00110",
"001001", and
"0000101"
are accepted, while the strings
"" (the empty string),
"0",
"1",
"00", and
"0011"
are rejected.
A computer scientist would say that this DFA accepts the
language of strings ending in "01" or
"10". Any language accepted by some DFA is called a
regular language. However, regular languages can be described
in many ways, and in some cases a short description in another
notation (eg a short regular expression) can lead to an immense
corresponding minimal DFA, and vice versa.
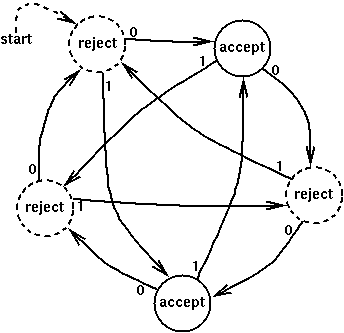This DFA accepts
strings of 0's and 1's in which the number
of 0's minus twice the number of 1's is
either 1 or 3 more than a multiple of 5. For instance, the strings
"1000", "0100", "0010",
"10111", "111101", "010000",
"100000", "0001101", and
"0000101" are accepted, while the strings
"101", "0000", "1101",
"00000", "00101", "010111", and
"1000111" are rejected.
In the problem of grammar induction, one is given a list (or ``corpus'') of strings labeled accepted or rejected, and one's task is to figure out the underlying rule. This is a ubiquitous problem: it crops up in computer translation, automatic proofreading, database querying, linguistics, computer speech recognition, cognitive psychology, and even computer vision and dynamic systems theory.
Even for languages accepted by DFAs, grammar induction becomes extremely difficult when there are not very many samples in the corpus relative to the size of the underlying DFA.
The first line is a header, giving the number of strings in the file (sixteen) and the number of symbols (0 and 1, which makes two). Each line after the header has the format ``label len sym1 ... symlen'' where len is the length of the string, and sym1 ... symlen are its symbols, separated by white space. The label 1 means accepted, and the label 0 means rejected. So the last line of the file indicates that the string 1000111 is rejected.16 2 1 4 1 0 0 0 1 4 0 1 0 0 1 4 0 0 1 0 1 5 1 0 1 1 1 1 6 1 1 1 1 0 1 1 6 0 1 0 0 0 0 1 6 1 0 0 0 0 0 1 7 0 0 0 1 1 0 1 1 7 0 0 0 0 1 0 1 0 3 1 0 1 0 4 0 0 0 0 0 4 1 1 0 1 0 5 0 0 0 0 0 0 5 0 0 1 0 1 0 6 0 1 0 1 1 1 0 7 1 0 0 0 1 1 1
The sample Trakhtenbrot-Barzdin DFA learning program, when provided with this training corpus file, prints out the following hypothesis DFA file. The first line is a header giving the number of states and the number of symbols. Each line after the header has the format ``state-number label 0-transition 1-transition.''
Now that we have run a learning algorithm and generated a hypothesis, we are in a position to propose a set of labels for the test set. The testing file looks just like a training file, except that the labels are -1, which means unknown.5 2 0 0 1 2 1 1 3 4 2 1 4 1 3 0 2 0 4 0 0 3
Suppose the testing file were this:
By stepping through the file and printing out the label that our hypothesis would assign to each of the 20 test strings, we would obtain the following 20-character string, which would be in the right format for submission to the Abbadingo Oracle: 1000100111001001100020 2 -1 7 0 0 1 1 0 0 0 -1 7 1 0 0 1 1 0 1 -1 7 1 0 1 0 1 0 1 -1 7 0 0 1 1 1 1 0 -1 7 0 1 0 0 1 0 1 -1 7 0 0 0 0 0 0 0 -1 6 1 0 1 0 0 1 -1 7 0 1 1 0 0 0 1 -1 7 1 0 0 0 0 1 0 -1 7 0 0 0 0 1 1 0 -1 5 0 0 0 1 0 -1 6 1 0 0 1 1 1 -1 6 0 0 0 0 0 1 -1 5 1 0 0 0 1 -1 7 1 1 1 0 1 1 1 -1 7 1 1 0 0 0 1 0 -1 7 1 0 0 0 0 0 1 -1 7 0 1 1 1 1 1 1 -1 7 1 0 0 1 1 1 1 -1 7 1 1 1 0 1 1 0
The testing set files for the real problems are much longer: each contains 1800 strings to be classified. To solve the problem and satisfy the Oracle, you must misclassify at most 18 of them.